算法导论之线性时间排序
寒假期间,由于新型冠状病毒疫情导致没法出门也没去练车,在家闲得开始学习,上学期结束了数据结构的课程,但是觉得还不够深入,而且学校的考试好简单…
遂决定自己在家看看《算法导论》补充点知识,毕竟是经典。看到前几章觉得自己学了个假数据结构,或者说曾经学了个假数学。研究了好久排序算法的时间复杂度,补充了一些证明相关的知识。写个博客记录一下~
非线性时间的排序算法
要证明基于比较的几种非线性时间的排序算法最低时间复杂度为O(nlgn),需要补充一个决策树的概念。(不知道为什么一个这么有用的模型我们数据结构课程都没有讲)
决策树概念
统计学,数据挖掘和机器学习中的决策树训练,使用决策树作为预测模型来预测样本的类标。 这种决策树也称作分类树或回归树。 在这些树的结构里, 叶子节点给出类标而内部节点代表某个属性。 在决策分析中,一棵决策树可以明确地表达决策的过程。
通过基于比较的事件来构建一个决策树模型,最终得到一个二叉树。(比较考虑两种结果大于或小于,所以最多只有两个子节点,而叶子结点则最终代表比较后的排序结果)
例如:
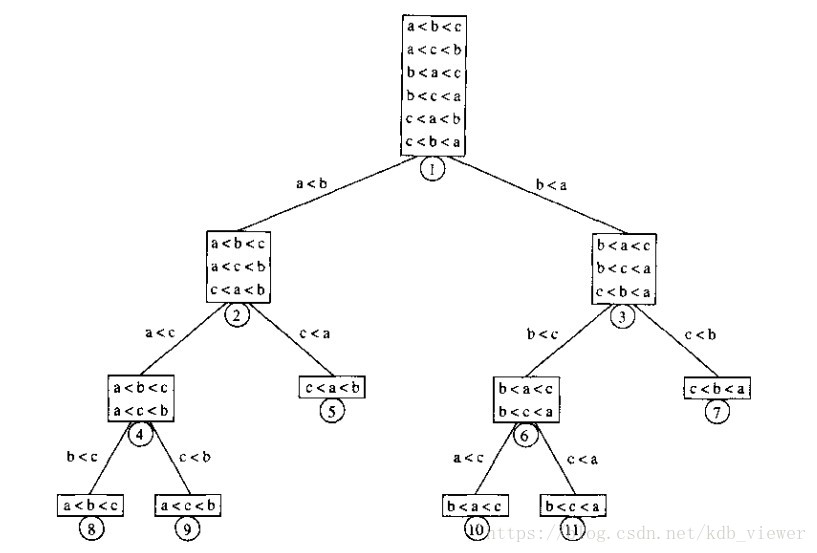
了解到决策树概念后,假设你的数据为n,则共有n!种排序结果,即决策树共有n!个叶子结点。
假设树的高度为h
则有
n! <= 2^h
h >= lg n!
斯特林公式引用
得出 算法下界为O(nlgn)
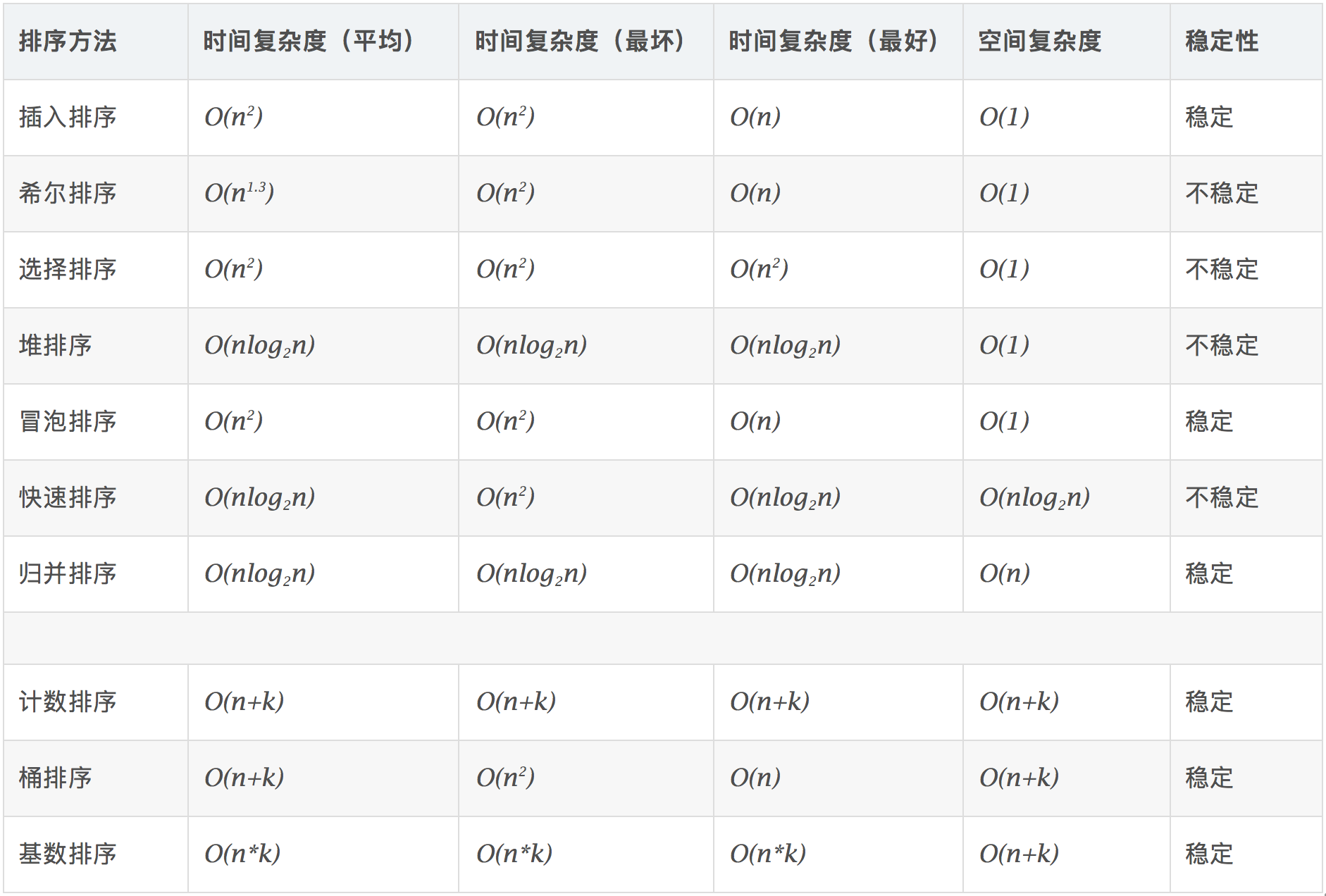
常见排序算法
前七种为常见的非线性时间排序算法,后三种为线性时间排序算法
不同的排序算法在不同的情况下会有差距较大的效果,不存在绝对的效率最高的算法。
线性时间的排序算法
接下来是关于两种线性时间的排序算法的相关证明。看起来线性时间的效果会高于非线性的算法,但当数据涉及范围非常大时,对于线性时间算法k占主导地位会导致效率大大降低。
计数排序算法
算法的步骤如下:
①找出待排序的数组中最大和最小的元素
②统计数组中每个值为i的元素出现的次数,存入数组C的第i项
③对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
④反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
其时间复杂度为O(k+n)。
数的范围为0~k, n为数的规模。它的时间复杂度是线性的,但复杂度不只是被数的规模所掌控,算法是否高效也取决于它的数的范围。
基数排序算法
基数排序的时间复杂度是O(kn),其中n是排序元素个数,k是数字位数。这不是说这个时间复杂度一定优于O(nlgn),k的大小取决于数字位的选择(比如比特位数),和待排序数据所属数据类型的全集的大小;k决定了进行多少轮处理,而n是每轮处理的操作数目。
以排序n个不同整数来举例,假定这些整数以B为底,这样每位数都有B个不同的数字,
k=logB N,N是待排序数据类型全集的势。虽然有B个不同的数字,需要B个不同的桶,但在每一轮处理中,判断每个待排序数据项只需要一次计算确定对应数字的值,因此在每一轮处理的时候都需要平均n次操作来把整数放到合适的桶中去
其中前一项是一个与输入数据无关的常数,当然该项不一定小于log n。
如果考虑和比较排序进行对照,基数排序的形式复杂度虽然不一定更小,但由于不进行比较,因此其基本操作的代价较小,而且在适当选择的B之下,k一般不大于log n,所以基数排序一般要快过基于比较的排序,比如快速排序。




